세그먼트 트리란?

11 분 소요

세그먼트 트리란?

고인물 알고리즘 중 하나인 세그먼트 트리이다.

A에서 B까지의 합을 구하는데 용이하게 쓰인다.

만약 문제에서 10만개의 집합에 대한 1~9만, 3만~8만의 합을 구하라 같은 질의가 여러번 오가게 된다면 합을 구하는데 어마어마한 시간이 걸릴것이다. 이럴때 쓰는게 바로 세그먼트 트리이다.

원리는 간단하다. 이진트리로 10개의 값이 있다면 1~5는 왼쪽, 6~10은 오른쪽으로 가게 되고, 1~5쪽은 또 1~2, 3~5로 나누고, 1~2 -> 1, 2로 나뉘는 식으로 각 구간을 절반으로 나누어서 합을 구한다.

세그먼트 트리는 이진트리로 구간을 절반씩 나눠 해당 구간에 대한 합을 저장한다.
구해 놓은 구간의 합을 이용해 구간합을 구할 수 있다 ex) 3~7의 구간합을 구하기 위해서 3~5, 6~7 구간합을 더해줄 수 있다.
중간에 해당 집합의 원소 값이 바뀌는 경우 바뀐 차이 만큼 해당 노드에 업데이트를 해준다.

예시

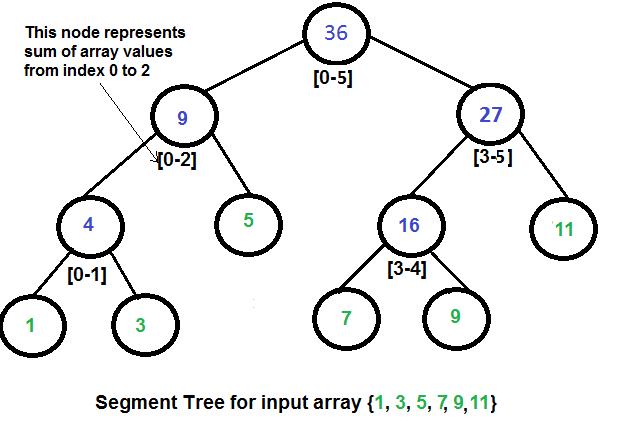
위 사진과 같이 루트 노드는 모든 집합의 합이다.

루트노드부터 시작하여 범위를 절반으로 나누어 구간합을 구해주어 세그먼트 트리를 만든다.

설명

세그먼트 트리의 크기를 할당해준다. ceil은 올리함수로 log2(N)의 값을 올림해준거에 + 1이 h가 되는데, 이 말은 즉슨 이진트리이기 완전한 이진트리 형태일때 필요한 노드의 개수만큼 할당해주겠다는 것이다. ex) n= 8 일때 모든 노드가 균형잡히게 할당되는데 이때 필요한 노드 개수가 8 + 4 + 2 + 1 = 15이다. 아래 공식대로 하면 16만큼 사이즈를 할당해주게 된다.
```
 SegmentTree(int N, long long* A) {
     int h = (int)ceil(log2(N));
     int node_size = 1 << (h + 1);
     nodes = new long long[node_size];

     this->A = A;
     init(0, 0, N - 1);
 }
```
init함수는 집합들을 이용해 초기 세그먼트 트리를 구성하는 함수 이다. start == end가 될때까지, 즉 원소가 하나 남을때까지 범위를 절반으로 나누어 재귀를 돌려준다. 그리고 남은 하나의 원소를 되돌려준다. 하나가 아닌 경우 해당 범위에 대한 합을 되돌리기 된다. nodes는 범위에 대한 값을 담는 배열이다.
```
 long long init(int index, int start, int end)
 {
     if (start == end)
         nodes[index] = A[start];
     else
         nodes[index] =
         init(2 * index + 1, start, (start + end) / 2) +
         init(2 * index + 2, (start + end) / 2 + 1, end);

     return nodes[index];
 }
```

left~right범위의 합을 구하는 함수이다. 구하는 범위가 밖에가면 그냥 0을 반환해주면 되구, 구하는 범위 내 인 경우 해당 구간합을 반환해준다. 두 경우 모두 아닌 경우 구간을 둘로 나누어주어 반환값을 합을 반환해준다.

 long long getSum(int index, int start, int end, int left, int right)
 {
     //구하려는 범위가 밖에 있는 경우
     if (left > end || right < start)
         return 0;
     else if (left <= start && right >= end)
         return nodes[index];

     int mid = (start + end) / 2;
     return getSum(index * 2 + 1, start, mid, left, right) +
         getSum(index * 2 + 2, mid + 1, end, left, right);
 }

바뀐 값의 차이 만큼(diff) changed_index가 범위 내에 들어가면 전부 값을 수정해준다.

 void update(int changed_index, long long diff, int index, int start, int end)
 {
     if (changed_index < start || changed_index > end)
         return;

     nodes[index] += diff;

     if (start != end) {
         int mid = (start + end) / 2;
         update(changed_index, diff, index * 2 + 1, start, mid);
         update(changed_index, diff, index * 2 + 2, mid + 1, end);
     }
 }

소스코드

#include <iostream>
#include <cmath>
using namespace std;

class SegmentTree
{
private:
	long long* nodes;
	long long* A;

	long long init(int index, int start, int end)
	{
		if (start == end)
			nodes[index] = A[start];
		else
			nodes[index] =
			init(2 * index + 1, start, (start + end) / 2) +
			init(2 * index + 2, (start + end) / 2 + 1, end);

		return nodes[index];
	}
public:
	SegmentTree(int N, long long* A) {
		int h = (int)ceil(log2(N));
		int node_size = 1 << (h + 1);
		nodes = new long long[node_size];

		this->A = A;
		init(0, 0, N - 1);
	}
	~SegmentTree() {
		delete[] nodes;
	}
	long long getSum(int index, int start, int end, int left, int right)
	{
		//구하려는 범위가 밖에 있는 경우
		if (left > end || right < start)
			return 0;
		else if (left <= start && right >= end)
			return nodes[index];

		int mid = (start + end) / 2;
		return getSum(index * 2 + 1, start, mid, left, right) +
			getSum(index * 2 + 2, mid + 1, end, left, right);
	}
	void update(int changed_index, long long diff, int index, int start, int end)
	{
		if (changed_index < start || changed_index > end)
			return;

		nodes[index] += diff;

		if (start != end) {
			int mid = (start + end) / 2;
			update(changed_index, diff, index * 2 + 1, start, mid);
			update(changed_index, diff, index * 2 + 2, mid + 1, end);
		}
	}
};

int main() {
	long long A[5] = { 1, 2, 3, 4, 5 };
	int distance[4][3] = {
		{1, 3, 6},
		{2, 2, 5},
		{1, 5, 2},
		{2, 3, 5}
	};

	SegmentTree st(5, A);

	for (int i = 0; i < 4; ++i) {
		// b번째 수를 c로 바꿈
		if (distance[i][0] == 1) {
			long long diff = distance[i][2] - A[distance[i][1]-1];
			A[distance[i][1] - 1] = distance[i][2];
			st.update(distance[i][1] - 1, diff, 0, 0, 5 - 1);
		}
		// b부터 c까지 수의 합 구함
		else {
			for (int i = 0; i < 5; ++i)
				cout << A[i] << ' ';
			cout << '\n';
			cout << distance[i][1] << "부터 " << distance[i][2] << "까지의 합 " 
				<< st.getSum(0, 0, 5 - 1, distance[i][1] - 1, distance[i][2] - 1) << '\n';
		}
	}
}

위의 소스는 뭐랄까 클래스로 정석적으로 짤때 소스이다. 이제 PS를 할때는 어떻게 짜는지 알아보자. 어떤 목적으로 짜느냐에 따라 조금씩 구조가 달라진다. 그렇다고 해서 개념적인게 바뀌는게 아니니 어떤부분이 다른지만 참고하면 좋을것 같다.

// 구간 합 세그
#include <iostream>
using namespace std;

const int MAXN = 10; // 최대 n크기가 10이라고 했을때 + 1(인덱스 0을 무시하고 짤때)
int tree[MAXN * 4]; // 최악의 경우 트리를 생성할때 약 n*4의 크기가 필요하다. 정적배열할땐 4배해주면 된다.
int node[MAXN + 1] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };


// 세그트리에 대한 정보가 한번에 주어지는 경우 node배열에 입력받아 한번에 초기트리를 생성하는 함수이다.
int init(int index, int start, int end) {
	// 시작지점과 끝이 같은 경우 리프노드인경우이다.
	// node에 담긴 값을 트리에 담고 값을 돌려준다.
	if (start == end)
		return tree[index] = node[start];
	// 리프노드가 아니라면 계속 뻗어나간다. 다 뻗어나간 후 구간합을 트리에 담는다.
	else {
		int mid = (start + end) / 2;
		return tree[index] = init(index * 2, start, mid) +
			init(index * 2 + 1, mid + 1, end);
	}
}

// 특정 인덱스의값이 diff만큼 바꿔었음을 업데이트 해준다.
void update(int index, int target, int diff, int start, int end) {
	if (target < start || target > end)
		return;
	tree[index] += diff;
	if (start == end)
		node[start] += diff; // 배열값 업데이트
	else {
		int mid = (start + end) / 2;
		update(index * 2, target, diff, start, mid);
		update(index * 2 + 1, target, diff, mid + 1, end);
	}
}

// left~right까지의 구간합을 구해준다,
int query(int index, int left, int right, int start, int end) {
	// 범위 벗어난경우 0반환
	if (left > end || right < start)
		return 0;
	// start, end가 범위 내이면 start~end구간합 반환
	// ex) 1~10의 구간합 구할때 3~7구간합 반환하면 1~2, 8~10구간합과 더하면됨
	if (left <= start && end <= right)
		return tree[index];
	else {
		int mid = (start + end) / 2;
		return query(index * 2, left, right, start, mid) +
			query(index * 2 + 1, left, right, mid + 1, end);
	}
}

int main() {
	init(1, 1, MAXN); // 세그트리 초기화
	// 2~5까지 합
	cout << "2부터 5까지의 구간합 " << query(1, 2, 5, 1, MAXN) << "\n";
	// 노드 4의값을 10으로 업데이트
	int target = 4, changeValue = 10;
	int diff = changeValue - node[target]; // 바뀌는 값과 차이를 구해줌
	update(1, target, diff, 1, MAXN);
	// 2 + 3 + 10 + 5 = 20
	cout << "2부터 5까지의 구간합 " << query(1, 2, 5, 1, MAXN) << "\n";
}

다음은 구간곱이다.

// 구간 곱 세그
// 곱세그의 경우 int 범위 넘기는 경우가 많다는걸 주의하자.
#include <iostream>
using namespace std;
const int MAXN = 10;

int node[MAXN + 1] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int tree[MAXN * 4];

int init(int index, int start, int end) {
	if (start == end)
		return tree[index] = node[start];
	else {
		int mid = (start + end) / 2;
		return tree[index] = init(index * 2, start, mid) *
			init(index * 2 + 1, mid + 1, end);
	}
}

// 곱 같은 경우는 값이 바뀔경우 +,-처럼 업데이트가 안되구 해당구간 재연산해줘야한다.
// 따라서 타겟의 범위에 벗어난 경우 해당 구간합을 return해준다. 왜냐하면 (해당 구간곱) * (업데이트 된 결과)가 부모노드의 결과이기 때문이다.
int update(int index, int target, int value, int start, int end) {
	if (target < start || target > end)
		return tree[index];
	if (start == end)
		return tree[index] = node[start] = value;
	else {
		int mid = (start + end) / 2;
		return tree[index] = update(index * 2, target, value, start, mid) *
			update(index * 2 + 1, target, value, mid + 1, end);
	}
}

// left~right까지의 구간곱을 구해준다,
int query(int index, int left, int right, int start, int end) {
	// 범위 벗어난경우 1반환(why? 1과 곱하면 값을 그대로~)
	if (left > end || right < start)
		return 1;
	// 구간 곱 반환
	if (left <= start && end <= right)
		return tree[index];
	else {
		int mid = (start + end) / 2;
		return query(index * 2, left, right, start, mid) *
			query(index * 2 + 1, left, right, mid + 1, end);
	}
}

int main() {
	init(1, 1, MAXN); // 세그트리 초기화
	// 2~5까지 곱
	cout << "2부터 5까지의 구간곱 " << query(1, 2, 5, 1, MAXN) << "\n";
	// 노드 4의값을 10으로 업데이트
	int target = 4, changeValue = 10;
	update(1, target, changeValue, 1, MAXN);
	// 2 * 3 * 10 * 5 = 300
	cout << "2부터 5까지의 구간곱 " << query(1, 2, 5, 1, MAXN) << "\n";
}

다음은 구간 MAX, MIN이다.(MAX와 MIN은 구현방식이 같으므로 MAX만 짜도록 하겠다.) 구조적으로 곱과 별로 다를게 없다.

// 구간 MAX 세그
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 10;

int node[MAXN + 1] = { 0, 5, 2, 3, 10, 1, 6, 7, 8, 9, 4 };
int tree[MAXN * 4];

int init(int index, int start, int end) {
	if (start == end)
		return tree[index] = node[start];
	else {
		int mid = (start + end) / 2;
		return tree[index] = max(init(index * 2, start, mid),
			init(index * 2 + 1, mid + 1, end));
	}
}

// max도 곱과 마찬가지로 값바뀔시 재연산 필요함
int update(int index, int target, int value, int start, int end) {
	if (target < start || target > end)
		return tree[index];
	if (start == end)
		return tree[index] = node[start] = value;
	else {
		int mid = (start + end) / 2;
		return max(tree[index] = update(index * 2, target, value, start, mid),
			update(index * 2 + 1, target, value, mid + 1, end));
	}
}

// left~right까지의 구간최대값을 구해준다,
int query(int index, int left, int right, int start, int end) {
	// 최대값을 구할것이니 최소값을 반환해주면된다(0이라 가정하고 넘겨주자, MIN인경우 INT_MAX같은 값이나 1e9넘겨주면 된다)
	if (left > end || right < start)
		return 0;
	if (left <= start && end <= right)
		return tree[index];
	else {
		int mid = (start + end) / 2;
		return max(query(index * 2, left, right, start, mid),
			query(index * 2 + 1, left, right, mid + 1, end));
	}
}

int main() {
	init(1, 1, MAXN); // 세그트리 초기화
	// 2, 3, 10, 1
	cout << "2부터 5까지의 구간 최대값 " << query(1, 2, 5, 1, MAXN) << "\n";
	// 노드 4의값을 1으로 업데이트
	int target = 4, changeValue = 1;
	update(1, target, changeValue, 1, MAXN);
	// 2, 3, 1, 1
	cout << "2부터 5까지의 구간 최대값 " << query(1, 2, 5, 1, MAXN) << "\n";
}

다음은 세그먼트트리의 합을 활용한 LIS 최장수열을 구하는 방식이다. 구간최댓값을 이용하여 푼다.

// 최장 수열 LIS 구하기
#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 10;

struct info {
	int val, idx;
	// 중복된 원소 처리를 위해 idx가 큰걸 우선처리 한다.
	bool operator < (const info& a) const {
		return (this->val == a.val ? this->idx > a.idx : this->val < a.val);
	}
};

int arr[MAXN + 1] = { 0, 10, 20, 10, 30, 20, 50, 60, 30, 40, 70 }; // 0인덱스는 버리는거로 가정
info node[MAXN + 1];
int tree[MAXN * 4];

void update(int index, int target, int value, int start, int end) {
	if (target < start || target > end)
		return;
	// 일반적인 구간최댓값을 구할땐 이렇게 하면 안된다.
	// 만약 기존 최댓값이 10이였는데 5로 바뀌었을때 구간 최댓값이 5로 업데이트 안되는 예외가 생길수 있다.
	// target이 포함된 노드의 최댓값을 업데이트 해준다고 생각하자.
	tree[index] = max(tree[index], value);
	if (start != end) {
		int mid = (start + end) / 2;
		update(index * 2, target, value, start, mid);
		update(index * 2 + 1, target, value, mid + 1, end);
	}
}

int query(int index, int left, int right, int start, int end) {
	if(left > end || right < start)
		return 0;
	if (left <= start && end <= right)
		return tree[index];
	else {
		int mid = (start + end) / 2;
		return max(query(index * 2, left, right, start, mid),
			query(index * 2 + 1, left, right, mid + 1, end));
	}
}

int main() {
	for (int i = 1; i <= MAXN; ++i) {
		node[i].val = arr[i];
		node[i].idx = i;
	}
	// 입력받은 값 기준으로 정렬
	sort(&node[1], &node[MAXN + 1]);

	// 값 작은 순서대로 업데이트
	for (int i = 1; i <= MAXN; ++i) {
		// 1~정렬전 인덱스값 범위에서 최댓값을 구함
		// 만약 값이 자신보다 작고, 정렬전 인덱스가 더 작았다면 MAX값으로 만나게됨
		int Max = query(1, 1, node[i].idx, 1, MAXN) + 1; // 찾은 MAX값에 + 1(자기 자신 포함)
		update(1, node[i].idx, Max, 1, MAXN); // 해당 MAX값을 정렬전 인덱스값에 업데이트
	}

	// 루트노드 출력
	// 10, 20, 10, 30, 20, 50, 60, 30, 40, 70
	// 10 20 30 50 60 70 -> 6
	cout << "최장 수열 길이 " << tree[1] << endl;
}

추가적으로 반복문으로 빠르고 쉽게 짜는 방식의 세그가 있다.. 알아두면 나름 쓸만할것 같다. 나는 안쓰것지만

https://codeforces.com/blog/entry/18051

참고자료

Twitter Facebook LinkedIn

ghdic

세그먼트 트리란?

세그먼트 트리란?

예시

설명

소스코드

참고자료

공유하기

댓글남기기

참고

라그랑주 미정계수법

공부조언글읽기

유튜브 중독 벗어나기 세팅 방법

내적과 외적