플로이드 와샬 알고리즘이란?

플로이드 와샬(Floyd Warshall)이란?

플로이드 와샬은 모든 정점에서 다른 모든 정점 사이의 최단 경로를 구하는 문제이다. 다 대 다의 최단 경로를 구할 경우 유용하게 쓰이며 엄청나게 심플하다. 시간 복잡도는 O(n^3)

• 다 대 다 최단거리를 구할 때 쓰는 알고리즘
• 음의 가중치를 가진 간선도 사용 가능
• 모든 정점에 대한 경로를 계산하므로 그래프가 아닌 2차원 배열 형태를 사용
• dp 방식으로 이전에 구한 값을 이용하여 갱신함

예시

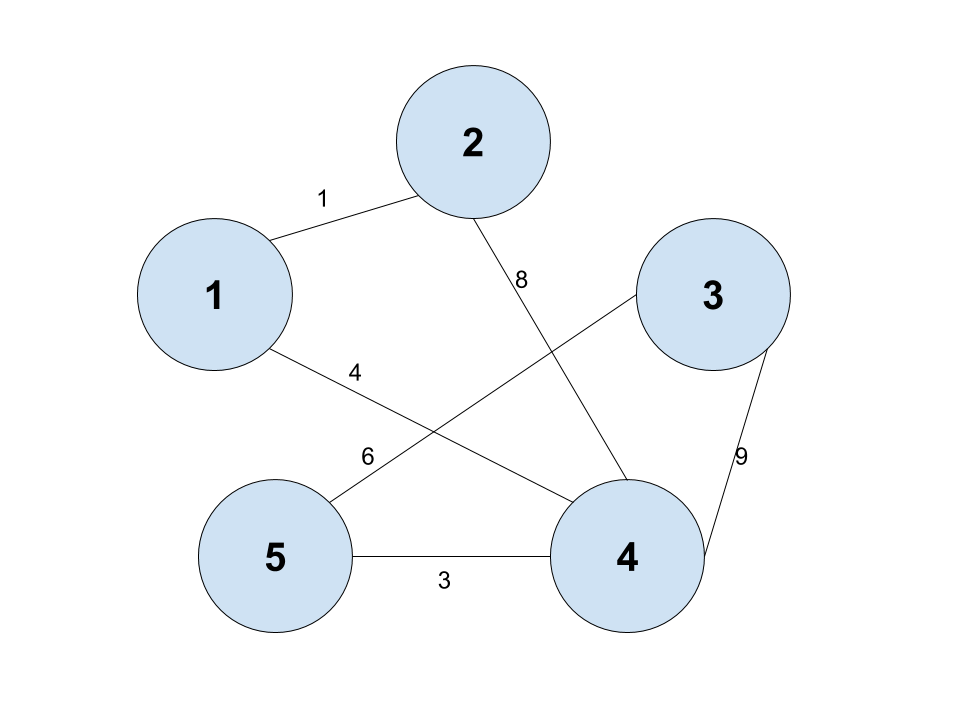
위와 같이 양방향 그래프가 있다고 하면 초기 상태는 2차원 배열로 이렇게 표현 될 수 있다.

x	1	2	3	4	5
1	0	1	INF	4	INF
2	1	0	INF	8	INF
3	INF	INF	0	9	6
4	4	8	9	0	3
5	INF	INF	6	3	0

설명

• 그냥 소스 돌려서 확인해보자(귀찮앙 언젠가 고치겠지??)

소스코드

#include <iostream>
using namespace std;

const int INF = 1e9;
int graph[5][5] = {
	{0, 1, INF, 4, INF},
	{1, 0, INF, 8, INF},
	{INF, INF, 0, 9, 6},
	{4, 8, 9, 0, 3},
	{INF, INF, 6, 3, 0}
};

int path[5][5];

void printPath(int v, int u) {
	if (path[v][u] == v)return;

	printPath(v, path[v][u]);
	cout << path[v][u]+1 << " ";
}

void printSolution() {
	for (int v = 0; v < 5; ++v) {
		for (int u = 0; u < 5; ++u) {
			if (u != v && path[v][u] != -1) {
				cout << v + 1 << "에서 " << u + 1 << "로 가는 가장 짧은길 -> " << v + 1 << ' ';
				printPath(v, u);
				cout << u + 1 << '\n';
			}
		}
	}
}

void print() {
	for (int i = 0; i < 5; ++i) {
		for (int j = 0; j < 5; ++j) {
			if (graph[i][j] == INF)
				cout << "INF ";
			else
				cout << graph[i][j] << ' ';
		}
		cout << '\n';
	}
}

void floydwarshall() {
	for (int v = 0; v < 5; ++v) {
		for (int u = 0; u < 5; ++u) {
			if (v == u)
				path[v][u] = 0;
			else if (graph[v][u] != INF)
				path[v][u] = v;
			else
				path[v][u] = -1;
		}
	}

	for (int by = 0; by < 5; ++by) {
		for (int from = 0; from < 5; ++from) {
			for (int to = 0; to < 5; ++to) {

				if (graph[from][by] + graph[by][to] < graph[from][to]) {
					graph[from][to] = graph[from][by] + graph[by][to];
					path[from][to] = path[by][to];
				}
			}

			// 대각의 원소가 음이 되면 음의 가중치 사이클이 생긴것
			if (graph[from][from] < 0) {
				cout << "음의 가중치 사이클 발견!\n";
				graph[from][from] = 0;
				cout << by + 1 << "번째 노드를 거쳐 가서 갱신" << endl;
				print();
				cout << '\n';
				return;
			}
		}
		cout << by + 1 << "번째 노드를 거쳐 가서 갱신" << endl;
		print();
		cout << '\n';
	}
}

int main() {
	cout << "초기 상태" << endl;
	print();
	floydwarshall();
	printSolution();
	return 0;
}

참고자료

• https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/