다익스트라(dijkstra) 알고리즘이란?
다익스트라 알고리즘이란?
다익스트라 알고리즘은 그래프에서 하나의 정점을 기준으로 다른점과의 최단거리를 구할때 유용한 알고리즘입니다. 시험에서도 유도과정을 구하는 문제로 나오는 단골문제이기도 하죠. 간단히 정리하면 아래와 같습니다.
- 하나의 정점을 기준으로 다른점들과의 최단거리를 구할때 쓴다.
- O(n*logn)의 시간 복잡도를 가진다.
- 거리가 음수가 아닐때 사용할 수 있다.
- 아직 가지 못하거나 못가는 곳은 INF로 표시된다.
예시
아래와 같은 그래프에서 최단거리를 탐색한다고 가정하자.
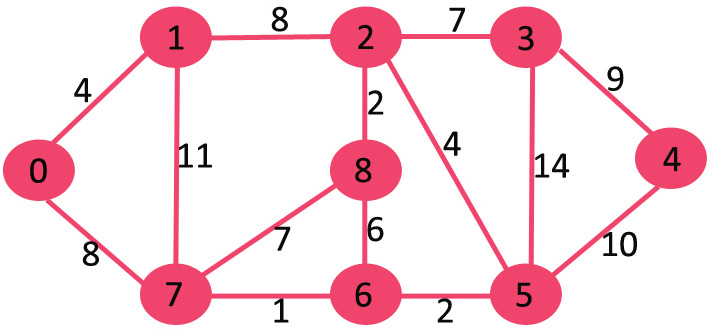
0인 노드에서부터 시작하여 0과 다른 노드간의 최단거리를 구할 것이다.
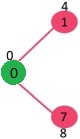
먼저 1 vs 7 노드로 가는길 중 1이 4로 더 작기 때문에 4노드를 탐색한다.
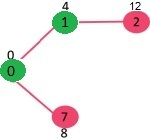
그 후 7노드로 가는 비용이 제일 작으므로 7선택
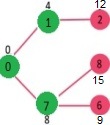
6 노드 선택
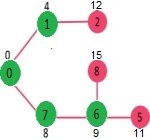
이런 식으로 뻗어나갈때 최소비용으로 뻗어나갈 수 있는 노드를 선택하면서 갱신해준다.
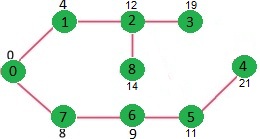
이러한 과정을 표로 표현하면 이렇게 된다.

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 0 | INF | INF | INF | INF | INF | INF | INF | INF |
| 0 | 4 | INF | INF | INF | INF | INF | INF | INF |
| 0 | 4 | INF | INF | INF | INF | INF | 8 | INF |
| 0 | 4 | INF | INF | INF | INF | 9 | 8 | INF |
| 0 | 4 | INF | INF | INF | 11 | 9 | 8 | INF |
| 0 | 4 | 12 | INF | INF | 11 | 9 | 8 | INF |
| 0 | 4 | 12 | INF | INF | 11 | 9 | 8 | 14 |
| 0 | 4 | 12 | 19 | INF | 11 | 9 | 8 | 14 |
| 0 | 4 | 12 | 19 | 21 | 11 | 9 | 8 | 14 |
설명
- 모든 정점과의 거리를 INF 초기화하고, 정점 0부터 출발한다.
- 이어져 있는 노드 중 최소 비용인것을 선택한다.
- 고른 노드를 통해 최솟값인 경우 갱신해주고 후보에 삽입해준다.
- 모든 노드를 탐색할때까지 반복한다.
소스코드
O(n^2)인 소스
#include <iostream>
using namespace std;
const int V = 9;
const int INF = 1e9;
// 방문하지 않은 정점 중 가장 비용이 작은 정점을 구하는 함수
int minDistance(int dist[], bool sptSet[]) {
int min = INF, min_index;
for (int v = 0; v < V; ++v) {
if (!sptSet[v] && dist[v] <= min) {
min = dist[v], min_index = v;
}
}
return min_index;
}
// 다익스트라를 통해 구한 한 정점에서 각 정점까지의 거리를 출력하는 함수
void printSolution(int dist[]) {
cout << "Vertex \t\t Distance from Source\n";
for (int i = 0; i < V; ++i)
cout << i << " \t\t " << dist[i] << '\n';
}
// 한 정점에서 다른 정점과의 최단거리를 구하는 함수
void dijkstra(int graph[V][V], int src) {
int dist[V]; // 최단거리를 담는 배열
bool sptSet[V]; // 해당 정점이 최단거리인지 알려주는 배열
// 모든 정점과의 거리를 INF로 초기화
for (int i = 0; i < V; ++i) {
dist[i] = INF, sptSet[i] = false;
}
// 시작 정점은 자신과의 거리 0
dist[src] = 0;
for (int count = 0; count < V - 1; ++count) {
// 최소 정점을 골라줌
int u = minDistance(dist, sptSet);
sptSet[u] = true;
// 해당 정점에서 다른 정점으로 가는 값이 기존의 값보다 작으면 갱신해줌
for (int v = 0; v < V; ++v) {
if (!sptSet[v] && graph[u][v] && dist[u] != INF
&& dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
}
printSolution(dist);
}
int main() {
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}
priority_queue를 이용하여 O(nlogn)인 소스
minDistance 함수를 priority_queue로 대체 했을뿐 그 외 다른건 없다.
#include <iostream>
#include <queue>
using namespace std;
const int V = 9;
const int INF = 1e9;
struct vertex {
int index, distance;
// 거리 작은 순으로 정렬
bool operator < (const vertex& v) const {
return this->distance > v.distance;
}
};
// 다익스트라를 통해 구한 한 정점에서 각 정점까지의 거리를 출력하는 함수
void printSolution(int dist[]) {
cout << "Vertex \t\t Distance from Source\n";
for (int i = 0; i < V; ++i)
cout << i << " \t\t " << dist[i] << '\n';
}
// 한 정점에서 다른 정점과의 최단거리를 구하는 함수
void dijkstra(int graph[V][V], int src) {
int dist[V]; // 최단거리를 담는 배열
bool sptSet[V]; // 해당 정점이 최단거리인지 알려주는 배열
priority_queue<vertex> pq; // 최단거리 순으로 반환하는 최소힙
// 모든 정점과의 거리를 INF로 초기화
for (int i = 0; i < V; ++i) {
dist[i] = INF, sptSet[i] = false;
}
// 시작 정점은 자신과의 거리 0
dist[src] = 0;
pq.push({ src, 0 });
while (!pq.empty()) {
int u = pq.top().index;
pq.pop();
sptSet[u] = true;
for (int v = 0; v < V; ++v) {
if (!sptSet[v] && graph[u][v] && dist[u] != INF
&& dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
pq.push({ v, dist[v] });
}
}
}
printSolution(dist);
}
int main() {
int graph[V][V] = { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
dijkstra(graph, 0);
return 0;
}


댓글남기기