벨만포드(bellmanford) 알고리즘

밸만포드 알고리즘이란?

다익스트라에서 음의 가중치를 두고 계산할 수 없던 점을 개선한 알고리즘, 대신해 다익스트라보다는 좀 더 느리다.

플로이드 워셜처럼 D(s,v) = D(s,u) + w(u,v) 방식으로 갱신해준다.

• 시간복잡도는 O(v*e) -> v는 정점, e는 간선
• 정점 개수만큼 반복을 돌릴때도 갱신이 되면 음의 사이클이 생긴것이다.
• 음의 가중치도 둘수 있음

예시

예시는 그리는게 귀찮으니 오늘도 geeksforgeeks껄로 가져왔다(고마워요 geeksforgeeks!)

시작 정점을 0으로 두고 나머진 INF로 둔다.

A->B, A->C, B->C로 가서 갱신된 경우

B->E, B->D, E->D 간선에 대한 갱신

설명

1. 각 정점과의 거리를 모두 INF로 초기화한다. 시작점은 0으로 초기화
2. 정점개수 - 1번만큼 반복한다.
   1. u->v로 가는 경로에 대하여 if dist[v] > dist[u] + weight인 경우 dist[v]를 업데이트 해준다.
3. 한번 더 위와 같이 도는데, 이때 dist값이 갱신될 경우 음의 가중치 사이클이 생긴것이다.(정점개수만큼 돌았을때 더 이상 갱신되면 안됨)

음의 가중치 사이클

그래프에서 노드가 연결되다 보면 사이클이 생길 수 밖에 없다. 이 때 사이클의 합이 양수인 경우는 if dist[v] > dist[u] + weight 조건문 때문에 갱신이 되지않으므로 문제가 되지 않는다.

하지만 음의 가중치인 경우는 어떨까? 아래 예시를 보자

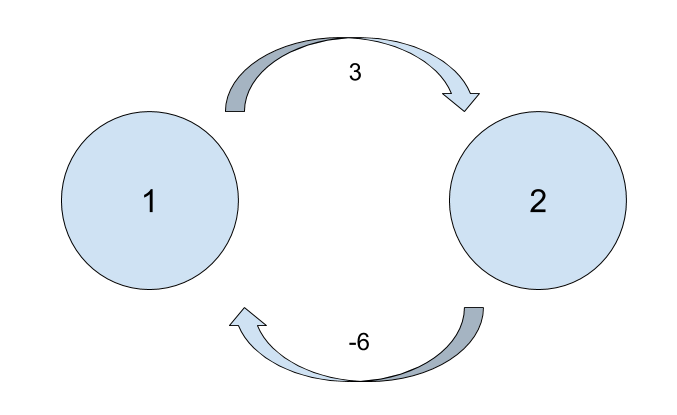
초기상태

	1	2
1	0	INF
2	INF	0

첫번째

	1	2
1	0	3
2	-3	0

두번째

	1	2
1	0	0
2	-6	0

세번째

	1	2
1	0	-3
2	-9	0

….

이런식으로 음의 사이클이 생기면 무한히 갱신이 되버린다.

그래서 벨만포드 알고리즘에서는 갱신이 안될때까지 돌리는 방식이 아닌 노드개수 - 1 번 갱신을 하고 한번더 갱신을 해봐서 이때 갱신이 되면 음의 사이클이 생기는 그래프라고 판단한다.

왜 노드개수 - 1 번이야?

노드개수 - 1번인 이유는 최악인 경우를 상정해보면 된다. 벨만포드 알고리즘은 모든 간선을 갱신해주는데… 아래와 같은 경우를 생각해볼수 있다.

위 예제에서 4번부터 시작해준다.

이때 간선은 앞에꺼부터 갱신을 해줄것이다. 우린 최악을 가정해야 되기때문이다.

dist	1	2	3	4
0번째	INF	INF	INF	0
1번째	INF	INF	1	0
2번째	INF	2	1	0
3번째	3	2	1	0

위처럼 최악의 경우를 상정할 경우 총 노드개수 - 1번 3번만에 갱신이 끝난다 앞의 간선부터 갱신할 경우 앞에꺼는 INF기 때문에 갱신이 안된다.

소스코드

다른 소스들은 adj[V]로 안나누고 그냥 vector에 간선들을 다 때려박고 돌리기 때문에 이중포문이다.

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct vertex {
	int dest, weight;
};

const int INF = 1e9;
const int V = 5;
const int E = 8;

vector<vertex> adj[V];
int dist[V];

int info[E][3] = {
	{0, 1, -1},
	{0, 2, 4},
	{1, 2, 3},
	{1, 3, 2},
	{1, 4, 2},
	{3, 2, 5},
	{3, 1, 1},
	{4, 3, -3}
};

void print() {
	for (int i = 0; i < V; ++i) {
		cout << i << "까지 최솟값 " << dist[i] << '\n';
	}
}

bool Bellmanford() {
	fill(&dist[0], &dist[V], INF);
	dist[0] = 0;

	// 정점개수만큼 반복
	for (int i = 1; i <= V; ++i) {
		// 각 정점을 갱신해줌
		for (int j = 0; j < V; ++j) {
			if (dist[j] == INF)continue;
			for (vertex& v : adj[j]) {
				if (dist[v.dest] > dist[j] + v.weight) {
					dist[v.dest] = dist[j] + v.weight;
					// 정점개수번째 돌때 갱신이 일어나면 음의 가중치 사이클이 생긴것
					if (i == V)return true;
				}
			}
		}
	}
	return false;
}

int main() {
	for (int i = 0; i < E; ++i) {
		adj[info[i][0]].push_back({ info[i][1] , info[i][2] });
	}
	cout << "음의 가중치 사이클 생김? -> " << (Bellmanford() ? "YES\n" : "NO\n");
	print();
}

참고자료

• https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/